Volumes
Grâce au calcul de volumes intégré à la plateforme, évaluez précisément les déblais/remblais, suivez l’évolution des vos sites ou quantifiez des stocks de matériaux en quelques clics. Cette fonctionnalité accessible depuis le navigateur simplifie vos workflows, élimine le besoin de logiciels lourds et favorise le partage d’analyses avec vos équipes et partenaires. Le calcul de volumes en ligne transforme vos données altimétriques en informations exploitables. Directement sur la plateforme, vous obtenez des résultats précis et partageables, pour des décisions plus rapides et une meilleure collaboration.
🛰️ Données nécessaires
Le calcul de volumes nécessite deux données d’entrée :
- Une donnée altimétrique, il peut s’agir d’un modèle numérique d’élévation (MNE) ou un modèle numérique de terrain (MNT), importée sur la plateforme. Ces données sont généralement obtenues par traitement de relevés photogrammétriques ou LiDAR avec des logiciels tels que Pix4d, Metashape ou QGIS.
- Un polygone issu d’un détourage manuel par l’utilisateur réalisé directement sur la plateforme.
🧮 Méthodes de calcul
Plusieurs méthodes de calculs sont proposées sur la plateforme afin de s’adapter au mieux à plusieurs cas de figures. Elles se basent tous sur un principe simple : une surface de base est déterminée selon un principe propre à la méthode de calcul employée, la différence d’altitude entre les données altimétriques déposées et ce plan de base constitue le volume calculé.
Pourquoi obtient on deux valeurs de volume ?
Afin de fournir un maximum d’informations et de permettre de connaître au mieux les données, chaque méthode de calcul fournit deux volumes :
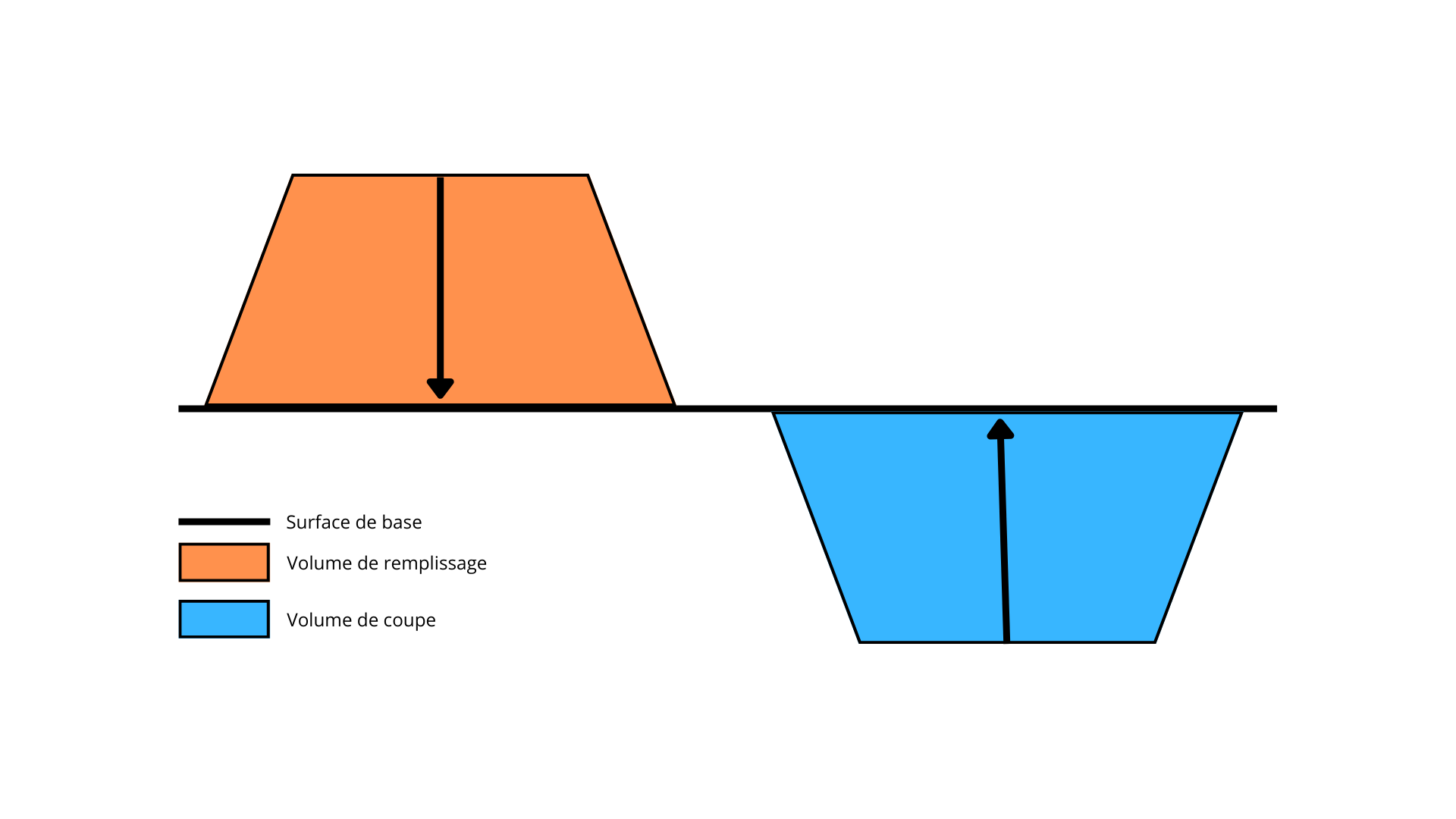
- Le volume de coupe : Il correspond au volume de matière à déblayer pour faire de la surface de base la surface réelle.
- Le volume de remplissage : Il correspond au volume de matière à remblayer pour aplanir la surface réelle à la surface de base.
Quelles sont les différences entre les méthodes de calculs de volumes ?
📐 Méthode de Triangulation
La méthode de triangulation détermine une surface de base théorique en utilisant le principe du Réseau Irrégulier Triangulé à partir des bords du polygone.
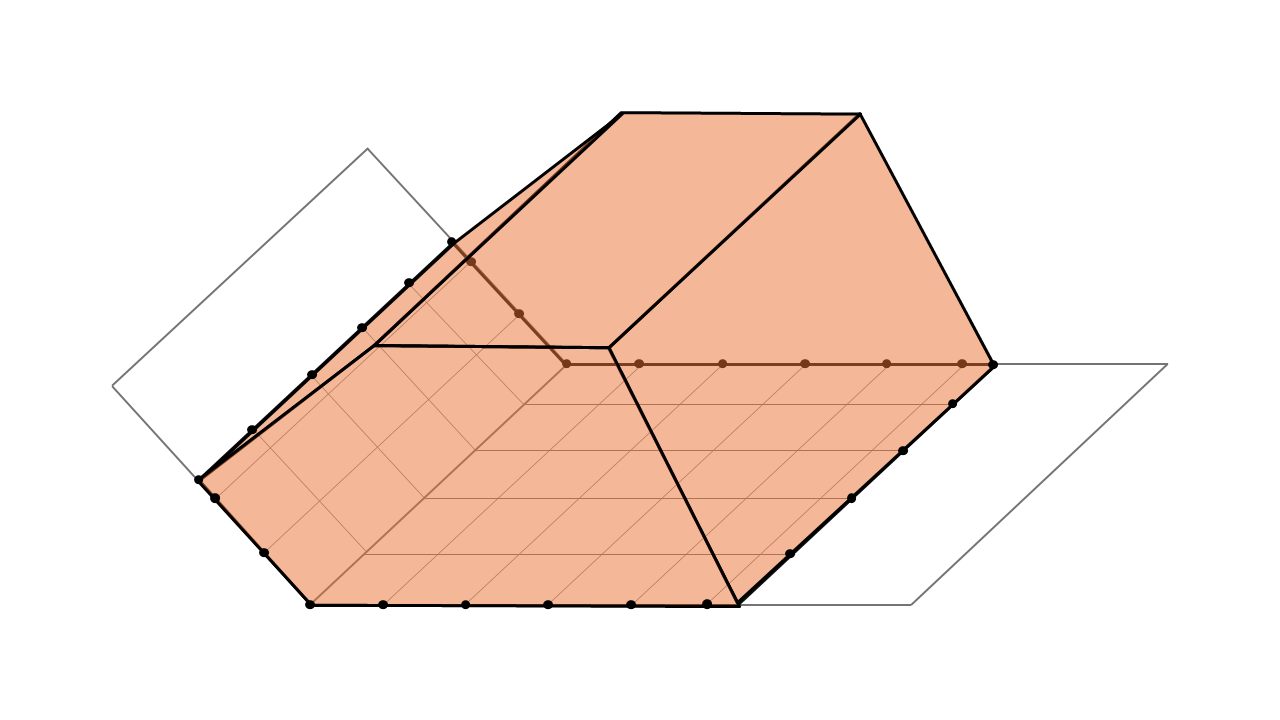
Volume de coupe obtenu avec la méthode de triangulation pour un stock de matériau sur un terrain irrégulier.
Cette méthode s’adapte aux terrains accidentés, épousant les reliefs complexes.
↘️ Méthode du Point Le Plus Bas
La méthode du point le plus bas calcule le volume entre le modèle de surface réel et un plan théorique défini par l’horizontale passant par le point le plus bas du polygone.
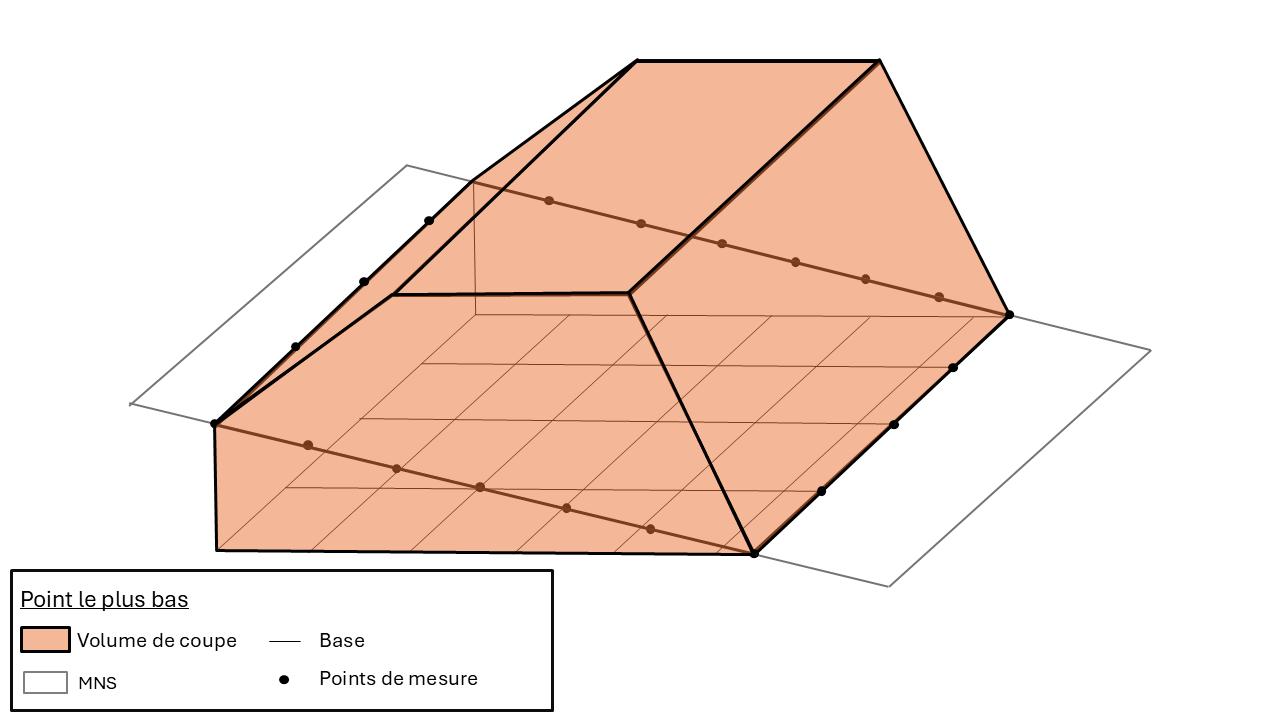
Volume de coupe obtenu avec la méthode de triangulation pour un stock de matériau sur un terrain en pente .
Dans des cas de terrains en pente, cette méthode surestime le volume de coupe. Cette méthode s’adapte le mieux aux terrains plats et horizontaux.
〰️ Méthode du Plan Moyenné
La méthode du plan moyenné définit un plan théorique minimisant la distance entre les points constitutifs du polygone et ce même plan.
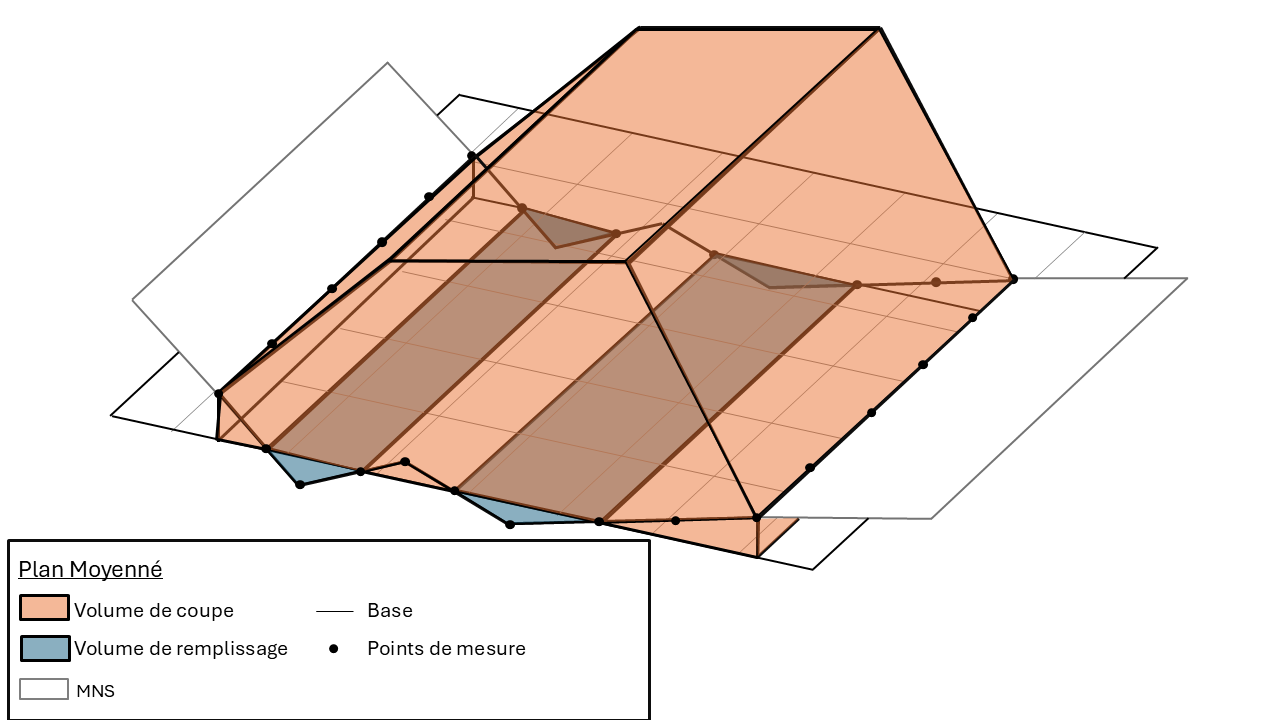
Volumes de coupe et de remplissage obtenus par la méthode du plan moyenné sur un terrain irrégulier.
Le volume de coupe est surestimé dans les zones où la base est localement haute et sous estimée dans les zones où la base est localement basse. En moyenne, sur des terrains présentant une rugosité de faible variation, les volumes sur et sous estimés se compensent.
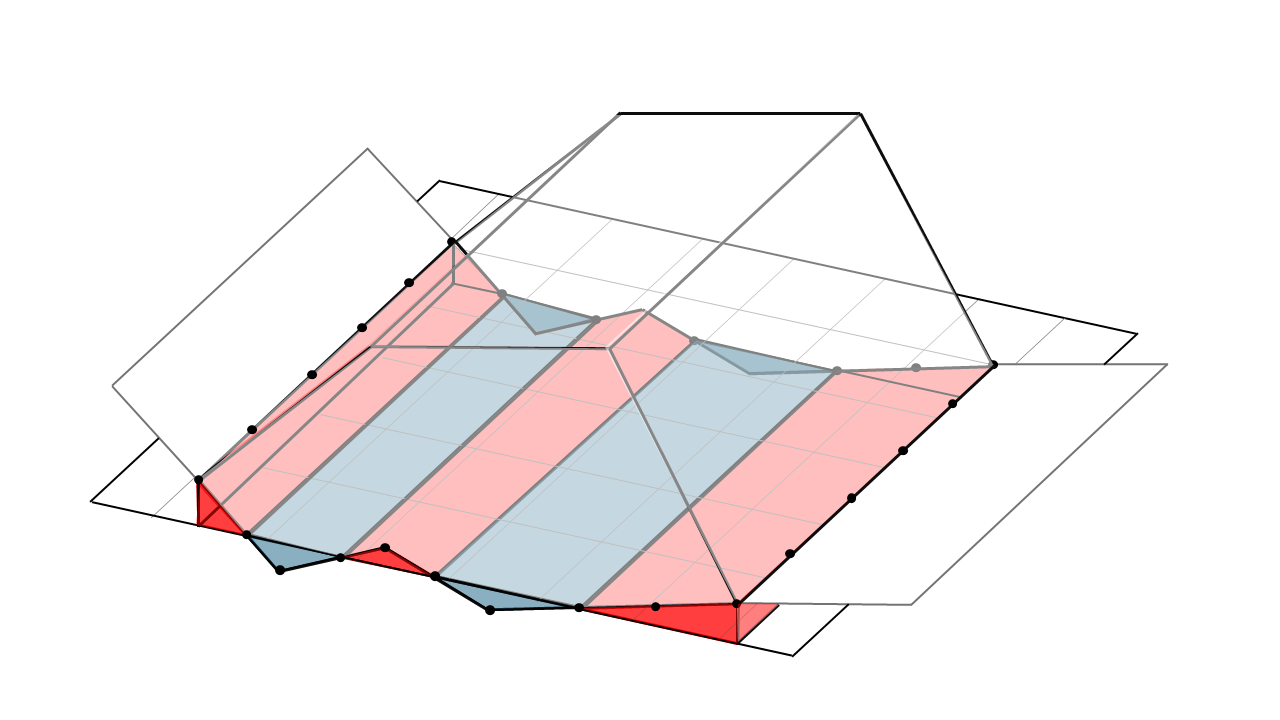
Volumes de coupe surestimés (rouge) et sous-estimés (bleu).
Le volume de coupe est donc calculé avec une bonne précision.
🔧 Méthode du Plan Personnalisé
La méthode du plan personnalisé définit un plan théorique horizontal correspondant à l’altitude entrée par l’utilisateur.
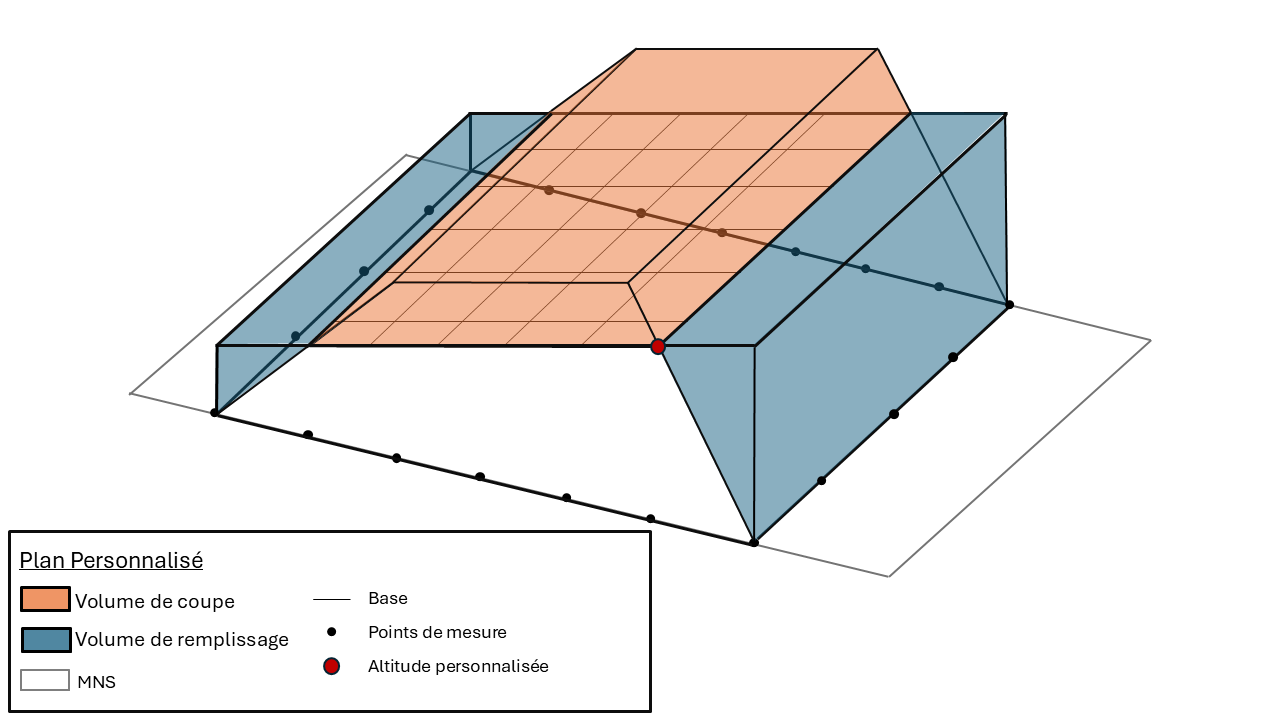
Volumes de remplissage et de coupure obtenus par la méthode du plan personnalisé pour un stock de matériaux en zone pentée.
↗️ Point le plus haut
La méthode du point le plus haut calcule le volume entre le modèle de surface réel et un plan théorique défini par l’horizontale passant par le point le plus haut du polygone.
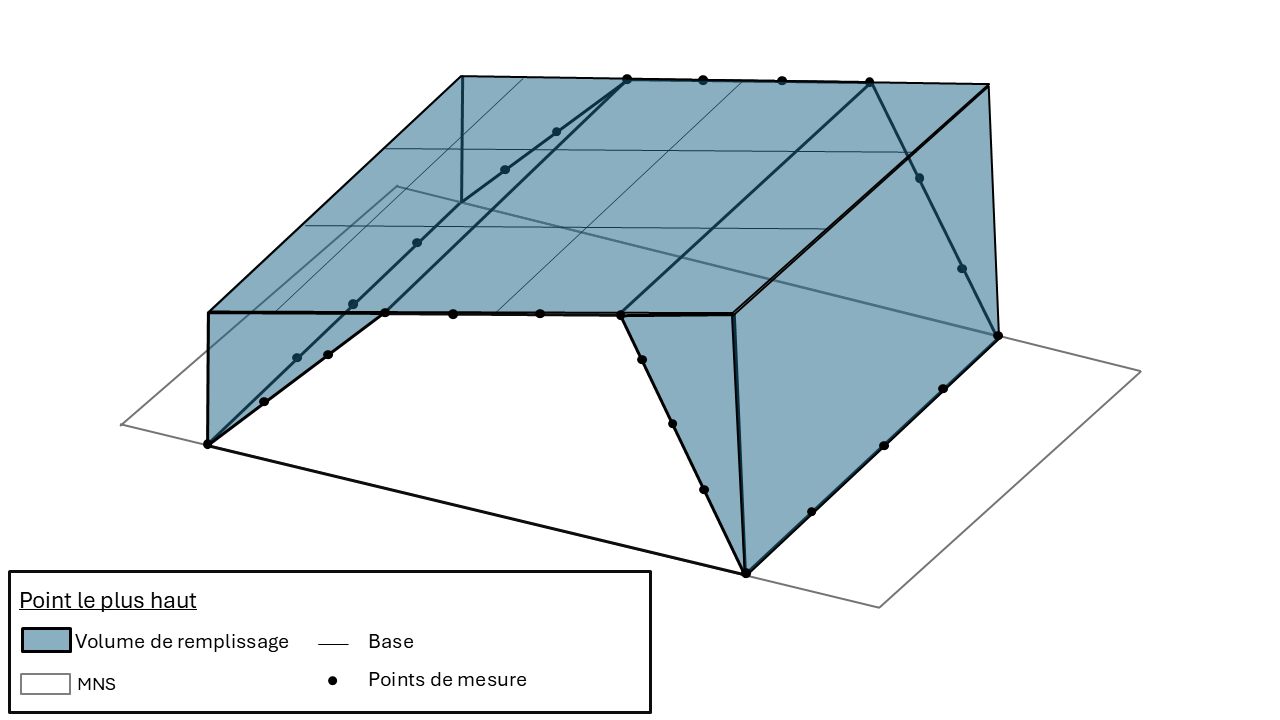
Volume de remplissage obtenu par la méthode du point le plus haut pour un stock de matériaux en zone pentée.
⚠️ Précautions
Utiliser la méthode adaptée est crucial pour obtenir des valeurs de volume cohérents, chaque méthode utilise une logique spécifique et s’adapte à un contexte particulier.
Avant de calculer un volume, il est conseillé de vérifier la présence de points aberrants qui pourraient totalement fausser les calculs.
Le nombre de points numérisés par l’utilisateur doit être suffisamment dense pour représenter avec précision les variations du terrain. Une distribution trop clairsemée peut entraîner une perte d’informations, conduisant à un calcul de volume imprécis.
📝 Résumé
| Méthode | Précision | Idéal pour |
|---|---|---|
| Triangulation | Très élevée | Terrains complexes, carrières |
| Point le plus haut | Élevée à Moyenne | Fosses, excavations |
| Plan moyenné | Élevée | Plateformes légèrement irrégulières, terrains en pente |
| Point le plus bas | Élevée à Moyenne | Dépôts de matériaux sur sol plat |
| Hauteur personnalisée | Élevée | Projets avec altitude de référence connue |